The next level above the SDDA establishes method specific data abstractions for the several different methods of solutions. The three higher level data abstractions which have been defined to date are dynamically hierarchical grids, hp-adaptive finite elements and dynamic trees. (Dynamic trees are the data abstractions upon which the fast multipole methods are implemented.)
Figure 7: Adaptive Grid Hierarchy - 2D (Berger-Oliger AMR Scheme)
Dynamically adaptive numerical techniques for solving differential equations provide a means for concentrating computational effort to appropriate regions in the computational domain. In the case of hierarchical adaptive mesh refinement (AMR) methods, this is achieved by tracking regions in the domain that require additional resolution and dynamically overlaying finer grids over these regions. AMR-based techniques start with a base coarse grid with minimum acceptable resolution that covers the entire computational domain. As the solution progresses, regions in the domain requiring additional resolution are tagged and finer grids are overlayed on the tagged regions of the coarse grid. Refinement proceeds recursively so that regions on the finer grid requiring more resolution are similarly tagged and even finer grids are overlayed on these regions. The resulting grid structure is a dynamic adaptive grid hierarchy. The adaptive grid hierarchy corresponding to the AMR formulation by Berger & Oliger [14] is shown in Figure 7.
Two basic distributed data-structures have been developed, using the fundamental abstractions provided by the SDDA (see Section 2, to support adaptive finite-difference techniques based on hierarchical AMR: (1) A Scalable Distributed Dynamic Grid (SDDG) which is a distributed and dynamic array, and is used to implement a single component grid in the adaptive grid hierarchy; and (2) A Distributed Adaptive Grid Hierarchy (DAGH) which is defined as a dynamic collection of SDDGs and implements the entire adaptive grid hierarchy. The SDDG/DAGH data-structure design is based on a linear representation of the hierarchical, multi-dimensional grid structure. This representation is generated using space-filling curves described in Section 2 and exploits the self-similar or recursive nature of these mappings to represent a hierarchical DAGH structure and to maintain locality across different levels of the hierarchy. Space-filling mapping functions are also used to encode information about the original multi-dimensional space into each space-filling index. Given an index, it is possible to obtain its position in the original multi-dimensional space, the shape of the region in the multi-dimensional space associated with the index, and the space-filling indices that are adjacent to it. A detailed description of the design of these data-structures can be found in [15].
Figure 8: SDDG Representation - Figure 9: DAGH Composite Representation
A multi-dimensional SDDG is represented as a one dimensional ordered list of SDDG blocks. The list is obtained by first blocking the SDDG to achieve the required granularity, and then ordering the SDDG blocks based on the selected space-filling curve. The granularity of SDDG blocks is system dependent and attempts to balance the computation-communication ratio for each block. Each block in the list is assigned a cost corresponding to its computational load. Figure 8 illustrates this representation for a 2-dimensional SDDG.
Partitioning a SDDG across processing elements using this representation consists of appropriately partitioning the SDDG block list so as to balance the total cost at each processor. Since space-filling curve mappings preserve spatial locality, the resulting distribution is comparable to traditional block distributions in terms of communication overheads.
The DAGH representation starts with a simple SDDG list corresponding to the base grid of the grid hierarchy, and appropriately incorporates newly created SDDGs within this list as the base grid gets refined. The resulting structure is a composite list of the entire adaptive grid hierarchy. Incorporation of refined component grids into the base SDDG list is achieved by exploiting the recursive nature of space-filling mappings: For each refined region, the SDDG sub-list corresponding to the refined region is replaced by the child grid's SDDG list. The costs associated with blocks of the new list are updated to reflect combined computational loads of the parent and child. The DAGH representation therefore is a composite ordered list of DAGH blocks where each DAGH block represents a block of the entire grid hierarchy and may contain more than one grid level; i.e. inter-level locality is maintained within each DAGH block. Figure 9 illustrates the composite representation for a two dimensional grid hierarchy.
The AMR grid hierarchy can be partitioned across processors by appropriately partitioning the linear DAGH representation. In particular, partitioning the composite list to balance the cost associated to each processor results in a composite decomposition of the hierarchy. The key feature of this decomposition is that it minimizes potentially expensive inter-grid communications by maintaining inter-level locality in each partition.
Figure 10: SDDG/DAGH Storage
Data-structure storage is maintained by the SDDA described in Section 2. The overall storage scheme is shown in Figure 10.
Figure 11: Programming Abstraction for Parallel Adaptive Mesh-Refinement
We have developed three fundamental programming abstractions using the
data-structures described above, that can be used to express parallel
adaptive computations based on adaptive mesh refinement (AMR) and
multigrid techniques (see Figure 11).
Our objectives are twofold: firstly, to provide application developers
with a set of primitives that are intuitive for implementing the problem,
i.e.
 .
.
The purpose of the grid geometry abstractions is to provide an intuitive means for identifying and addressing regions in the computational domain. These abstractions can be used to direct computations to a particular region in the domain, to mask regions that should not be included in a given operation, or to specify region that need more resolution or refinement. The grid geometry abstractions represent coordinates, bounding boxes and doubly linked lists of bounding boxes.
The coordinate abstraction represents a point in the computational domain. Operations defined on this class include indexing and arithmetic/logical manipulations. These operations are independent of the dimensionality of the domain.
Bounding boxes represent regions in the computation domain and is comprised of a triplet: a pair of Coords defining the lower and upper bounds of the box and a step array that defines the granularity of the discretization in each dimension. In addition to regular indexing and arithmetic operations, scaling, translations, unions and intersections are also defined on bounding boxes. Bounding boxes are the primary means for specification of operations and storage of internal information (such as dependency and communication information) within DAGH.
Lists of bounding boxes represent a collection of regions in the computational domain. Such a list is typically used to specify regions that need refinement during the regriding phase of an adaptive application. In addition to linked-list addition, deletion and stepping operation, reduction operations such as intersection and union are also defined on a BBoxList.
The grid hierarchy abstraction represents the distributed dynamic adaptive grid hierarchy that underlie parallel adaptive applications based on adaptive mesh-refinement. This abstraction enables a user to define, maintain and operate a grid hierarchy as a first-class object. Grid hierarchy attributes include the geometry specifications of the domain such as the structure of the base grid, its extents, boundary information, coordinate information, and refinement information such as information about the nature of refinement and the refinement factor to be used. When used in a parallel/distributed environment, the grid hierarchy is partitioned and distributed across the processors and serves as a template for all application variables or grid functions. The locality preserving composite distribution [16] based on recursive Space-filling Curves [17] is used to partition the dynamic grid hierarchy. Operations defined on the grid hierarchy include indexing of individual component grid in the hierarchy, refinement, coarsening, recomposition of the hierarchy after regriding, and querying of the structure of the hierarchy at any instant. During regriding, the re-partitioning of the new grid structure, dynamic load-balancing, and the required data-movement to initialize newly created grids, are performed automatically and transparently.
Grid Functions represent application variables defined on the grid hierarchy. Each grid function is associated with a grid hierarchy and uses the hierarchy as a template to define its structure and distribution. Attributes of a grid function include type information, and dependency information in terms of space and time stencil radii. In addition the user can assign special (Fortran) routines to a grid function to handle operations such as inter-grid transfers (prolongation and restriction), initialization, boundary updates, and input/output. These function are then called internally when operating on the distributed grid function. In addition to standard arithmetic and logical manipulations, a number of reduction operations such as Min/Max, Sum/Product, and Norms are also defined on grid functions. GridFunction objects can be locally operated on as regular Fortran 90/77 arrays.
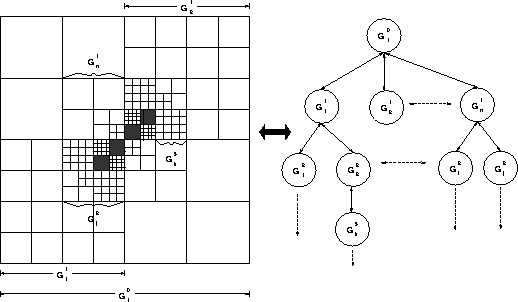
The hp-adaptive finite element mesh data structure consists of two layers of abstractions, as illustrated in Figure 12. The first layer consists of the Domain and Node abstractions. The second layer consists of mesh specific abstractions such as Vertex, Edge, and Surface, which are specializations of the Node abstraction.
Figure 12: Layering of Mesh Abstractions
A mesh Domain is the finite element application's specialization of the SDDA. The Domain uses the SDDA to store and distribute a dynamic set of mesh Nodes among processors. The Domain provides the mapping from the N-dimensional finite element domain to the one-dimensional index space required by the SDDA.
A finite element mesh Node associates a set of finite element basis functions with a particular location in the problem domain. Nodes also support inter-Node relationships, which typically capture properties of inter-Node locality.
Specializations of the finite element mesh Node for a two-dimensional problem are summarized in the following table and illustrated Figure 13.
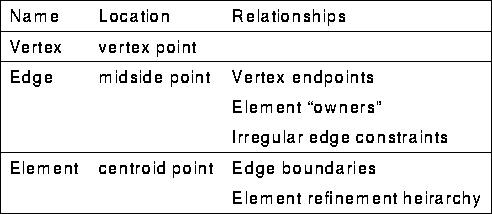
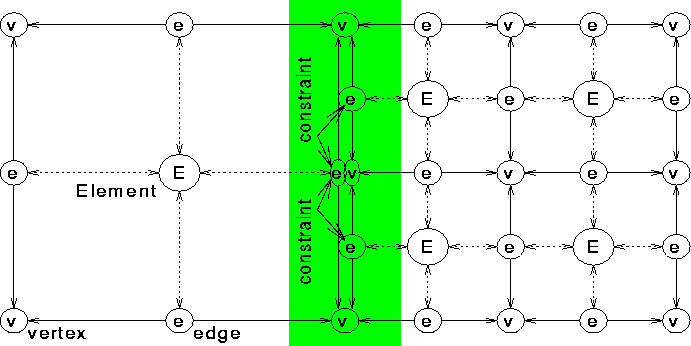
Figure 13: Mesh Object Relationships
Extended relationships between mesh Nodes are obtained through the minimul set of relationships given above. For example:
 Vertex =
Element
Vertex =
Element Edge
Edge Vertex
Vertex
 Element =
Element
Element =
Element Edge
Edge Element (normal)
Element (normal)
 Element =
Element
Element =
Element Edge
Edge Edge
Edge Element (constrained)
Element (constrained)
Finite element h-adaptation consists of splitting elements into smaller elements, or merging previously split elements into a single larger elements. Finite element p-adaptation involves increasing or decreasing the number of basis functions associated with the elements. An application performs these hp-adaptations dynamically in response to an error analysis of a finite element solution.
HP-adaptation results in the creation of new mesh Nodes and specification of new inter-Node relationships. Following an hp-adaptation the mesh partitioning may lead to load imbalance, as such the application may repartition the problem. The SDDA significantly simplifies such dynamic data structure update and repartitioning operations while insuring data structure consistency throughout these operations.
An adaptive distributed tree requires two main pieces of information. First it needs a tree data structure with methods for gets, puts, and pruning nodes of the tree. This infrastructure requires pointers between nodes. Second an adaptive tree needs an estimation of the cost associated with each node of the tree in order to determine if any refinement will take place at that node. With these two abstractions, an algorithm can utilize an adaptive tree in a computation. At this point, we are developing a distributed fast multipole method based on balanced trees, with the goal of creating a mildly adaptive tree in the near future.
All references in the tree are made through a generalization of the pointer concept. These pointers are implemented as keys into the SDDA, and access is controlled by accessing the SDDA data object with the appropriate action and key. This control provides a uniform interface into a distributed data structure for each processor. Thus, distributed adaptive trees are supported on the SDDA.
The actual contents of a node includes a list of items.