Introduction

Overview and Motivation

This paper defines, describes and demonstrates the application of a computational infrastructure which is an effective basis for development of parallel adaptive methods for the solution of systems of partial differential equations. While space restrictions limits the depth of coverage of the several elements of the infrastructure we felt it to be important to describe the full infrastructure and the motivating applications. URLs for web sites where additional information on each subject can be found are given in the discussions of each element of the infrastructure.

The motivations for this research are:

1. Adaptive methods will be utilized for the solution of almost all very large-scale science and engineering models. These adaptive methods will be executed upon the very large-scale heterogeneous parallel execution environment.

2. Effective application of these complex methods on scalable parallel architectures will be possible only through the use of programming abstractions which lower the complexity of application structures to a tractable level.

3. A common infrastructure for this family of algorithms will result in both enormous savings in coding effort but also a more effective infrastructure due to pooling and focusing of effort.

This infrastructure has been developed as a result of collaborative research among computer scientists, computational scientists and application domain specialists working on three different projects: An ARPA project for hp-adaptive computational fluid dynamics and two NSF sponsored Grand Challenge projects, one for numerical relativity and another on composite materials. The computational infrastructure is being used at several sites of the numerical relativity Grand Challenge project.

Conceptual Framework

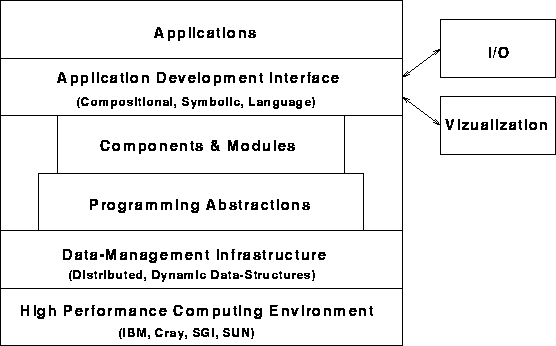
Figure 1 is a schematic of our perception of the structure of solution codes for sets of partial differential equations. This paper is primarily concerned with the lowest two layers of this hierarchy and how these layers can support implementation of higher levels of abstraction. These two elements are a data management layer which implements an array abstraction and a programming abstraction layer which implements data abstractions such as grids, meshes and trees which underlie different solution methods. The clean separation of array semantics from the higher level operations is critical to the success of this approach in providing a foundation for several different solution methods. Each project used a different adaptive solution method. The data management infrastructure is founded on the observation that several different adaptive methods for solution of partial differential equations have a common set of requirements for management of the dynamic distributed data structures which ensue from the adaptation and parallelization of the solution. In particular it will be shown that finite difference methods based on adaptive mesh refinement, hp- adaptive finite element methods and adaptive fast multipole methods for solution of linear systems can readily be implemented on the scalable dynamic distributed array (SDDA) data structure.

Properties of the SDDA include:

1. Single processor semantics are preserved - The dynamism and distribution of the array and the communication requirements engendered by distribution are transparent to computational operations

2. The index space of the array is directly derived from the geometry of the problem.

3. The mapping of the n-dimensional index space to the one- dimensional space of linear memory preserves the locality of the problem geometry.

4. The arrays are hierarchical and dynamic in both the number of levels in the hierarchical definition and with respect to size at any level.

5. Performance of applications built on the SDDA are competitive, in fact, often superior to those programmed in conventional languages such as C and Fortran 90.

Figure 1: Hierarchical Structure for Solution Systems for Partial Differential Equations

Related Work

There is a rich spectrum of previous work, some focusing on support for specific adaptive solution methods [1] and several systems which implement distributed arrays, grids or matrices ([6][5][4][3][2]). The two lowest levels of the computational infrastructure, the SDDA and the programming abstractions, are an evolutionary development which owe significant intellectual debts to the previous systems. The extensions of the infrastructure presented herein over previous implementations are:

1. broader support for dynamic structuring,
2. preservation of geometric locality of the problem in the storage structure and
3. more importantly, a clean separation of data management issues from programming abstraction issues abstraction issues.

Problem Specification

Adaptive algorithms require definition of operators on complex dynamic data structures. Two problems arise: (i) the volume and complexity of the bookkeeping code required to format the data structures overwhelms the actual computations and (ii) maintaining locality under expansion and contraction of the arrays requires complex copying operations if standard storage layouts are used. Implementation on parallel and distributed execution environments adds the additional complexities of partitioning, distribution and communication. Application domain scientists and engineers are forced to create complex data management capabilities which are far removed from the application domain. Additionally the standard parallel programming languages do not provide explicit support for dynamic distributed data structures.

Goal and Approach

The goal for this research is to reduce the intrinsic complexity of coding of parallel adaptive algorithms by providing an appropriate set of data structures and programming abstractions. Several versions of this infrastructure are available on the Web. It will be made available as an "STL-like" class library.

This research has been executed as collaborations among computer scientists, computational scientists and application domain researchers on three different projects. This collaboration is of critical importance to the development of the infrastructure. It has been repeated found during the development to date that the applications cannot foresee their requirements for implementation of a given method prior to implementation and that the computer and computational scientists cannot predict what is needed for the implementation of a given method.