Intercommutation of
Semilocal Strings and Skyrmions
Pablo Laguna
Department of Astronomy & Astrophysics, IGPG, CGWP
Penn State University, University Park, PA 16802
Vishnu Natchu and Richard A. Matzner
Center for Relativity, Department of Physics
The University of Texas at Austin, Austin, TX 78712
Tanmay Vachaspati
CERCA, Department of Physics
Case Western Reserve University,10900 Euclid Avenue, Cleveland, OH
44106-7079
Abstract:
We study the intercommuting of semilocal strings and Skyrmions, for a
wide range of internal parameters, velocities and intersection angles
by numerically evolving the equations of motion. We find that the
collisions of strings and strings, strings and Skyrmions, and Skyrmions
and Skyrmions, all lead to intercommuting for any set of parameters.
Even the collisions of unstable Skyrmions and strings leads to
intercommuting, demonstrating that the phenomenon of intercommuting is
very robust, extending to dissimilar field configurations that are not
stationary solutions. Even more remarkably, at least for the
semilocal formulation considered here, all intercommutations
trigger a reversion to U(1) Nielsen-Olesen strings.
Movies of Simulations:
Movies are generated as isometric views with the camera at 45 degress elevation and 45 degree rotation about the z axis.
Click on the images to access the movie files.
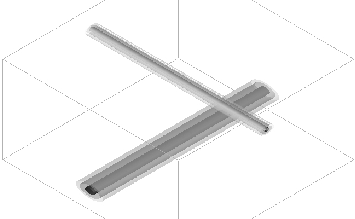
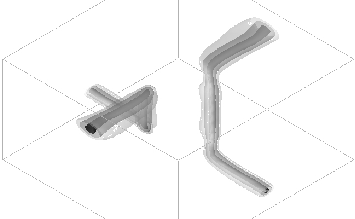
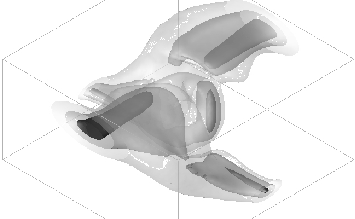
Figure 1:
Field 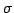 for a collision of
for a collision of 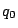 = 1 ("top") and
= 1 ("top") and
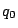 =3 semilocal strings, at
=3 semilocal strings, at
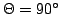 , with collision
velocity V= 0.9. The contours are
, with collision
velocity V= 0.9. The contours are 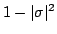 at values 0.1, 0.2, 0.5. Note that
at values 0.1, 0.2, 0.5. Note that
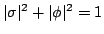 is the
vacuum. The strings reconnect.
is the
vacuum. The strings reconnect.
|
Figure 2:
Coincident configurations of the field 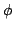 in the collision of
FIG 1. The contours are
in the collision of
FIG 1. The contours are 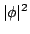 at 0.2, 0.3, 0.5. The value
at 0.2, 0.3, 0.5. The value 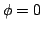 is an NO string. It can be seen that the configurations reverts to NO form
after the collision.
This is in spite of the fact our boundary conditions hold
the boundary values of the strings in their original
is an NO string. It can be seen that the configurations reverts to NO form
after the collision.
This is in spite of the fact our boundary conditions hold
the boundary values of the strings in their original  =1 and
=1 and 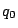 =3
state. The transition from the initial value of
=3
state. The transition from the initial value of 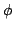 to the value of zero
means we have two NO strings near the center terminating on the (outward
moving) ends of the
to the value of zero
means we have two NO strings near the center terminating on the (outward
moving) ends of the 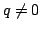 semilocal strings.
semilocal strings.
|
Movie simulations for other parameter values can be viewed below
|
|
q (top string) = 0.0
|
q (top string) = 1.0
|
|
q (bottom string) = 0.0
|
X
|
X
|
|
q (bottom string) = 1.0
|
|



