Source Code

The source code used for the five point stencil can be obtained here implicit.f The subroutines solve1 and impl_update1 set up and solve the matrices for the five-point stencil. except for additional routines for periodic and radiation boundaries.

Data for five point stencil

The runs that follow were carried out with
****Parameters****
nx(1,2,3) = 201 401 801
xmin/max= -1.0 1.0
gaussian width = 5.0E-02
gaussian amplitude = 0.5
propagation velocity = 1.0
dt/dx = cfl = 1.0
max no. of iterations to run 200
final time = 2.00
reciprocal condition number of matrix = 0.2

Reflecting Boundaries

Evolution with Reflecting boundaries
Given the initial data discussed in project II and parameters discussed earlier an evolution is carried out to 200 steps. This corresponds to a time of 2.00 units. The pulse moves to the right and when it hits the boundaries it is reflected as expected. The evolving pulse decays rapidly in time. The rate of decay is faster for coarser grids. The convergence factor is seen to decay rapidly below 2. We would have expected, from our analysis from project III, that the convergence factor should remain around 2.0 but due to the dissipation of the wave we get the decay. In the movies that follow I show an evolution with 801 points and 201 points. The yellow curve shows the 201 point evolution and the blue the 801.

MPEG movie of evolution of moving pulse with reflecting boundaries for the five point scheme.

Reflecting boundary convergence test
The graph below shows the convergence factor as a function of time. The convergence factor decays as a function of time At t=1.0 the variation is due to boundary conditions.


Source Code

The source code used for the nine point stencil is in the same file as in the case of the five point stencil. The subroutines solve2 and impl_update2 set up and solve the matrices for the nine-point stencil. The source for this can be obtained from this link except for additional routines for periodic and radiation boundaries.

Data for nine point stencil

The runs that follow were carried out with
****Parameters****
nx(1,2,3) = 201 401 801
xmin/max= -1.0 1.0
gaussian width = 5.0E-02
gaussian amplitude = 0.5
propagation velocity = 1.0
dt/dx = cfl = 1.0
max no. of iterations to run 200
final time = 2.00
condition number of matrix = 1.0

Reflecting Boundaries

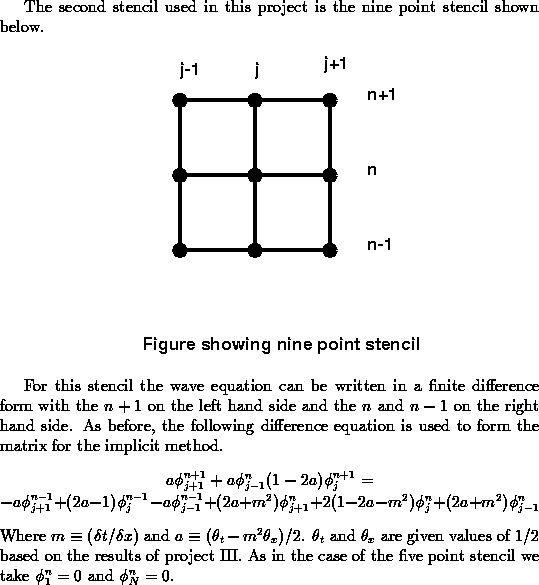
Evolution with Reflecting boundaries
Given the initial data discussed in project II and parameters discussed earlier an evolution is carried out to 200 steps. This corresponds to a time of 2.00 units. The pulse moves to the right and when it hits the boundaries it is reflected as expected. Note that compared to the five point stencil this evolution does not dissipate as drastically. The convergence factor stays near an even 4.08 except when the waves hit the boundaries at t=1 and t=2 units. For these runs I took theta_t = 1/2 and theta_x = 1/2.
In the movies that follow I show an evolution with 801 points. The first shows the function phi itself and the second the truncation error estimate in phi. The truncation error estimate was obtained by subtracting phi_2h from phi_h. It is interesting to note that the truncation error estimate consists of two sets of pulses which are opposite in sign. At t=2.0 They cancel. Perhaps this might aid in explaining the drop in the convergence factor at that time.

MPEG movie of evolution of moving pulse with reflecting boundaries for the nine point scheme.
MPEG movie showing the truncation error estimate in time.

Reflecting boundary convergence test
The graph below shows the convergence factor as a function of time. At t=1.0 and t=2.0 there are drops in the convergence factor due to the fact that the truncation error drops to zero at t=1.0 and t=2.0. The explanation can be that (phi_4h - phi_2h) goes to zero faster than (phi_2h - phi_h) at t=1.0,2.0,3.0,... and so the ratio goes to zero. An alternative, suggested by S. Liebling, is to subtract four times (phi_2h - phi_h) from (phi_4h - phi_2h) and show that as a function of time.