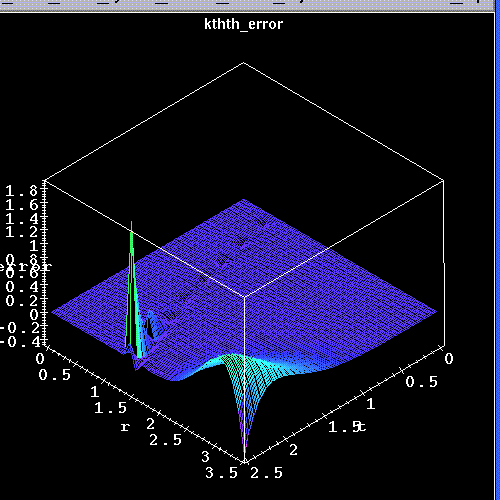
This plot shows the angular component of the extrinsic curvature as a function of r and t resulting from our numerical evolution code. Here the coordinate r corresponds to an isotropic radial coordinate which is locked to the Novikov radial coordinate for our case of geodesic slicing. The coordinate t is simply the proper time. These values of the angular component of the extrinsic curvature are reduced data computed from the cartesian extrinsic curvature components which the code evolves directly. We chose the diagonal of our 3D computational grid to provide us a radius along which we could compute this representative plot. The region from r=0 to r~1.0 is the excised interior of the event horizon which can be seen expanding in coordinate space as time advances.

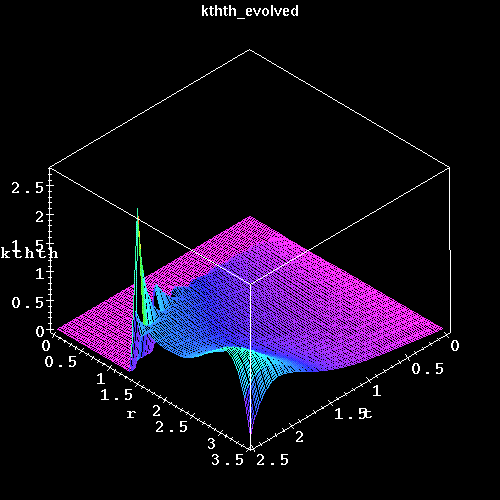
Similarly, this is a plot of the exact solution of the angular extrinsic curvature component in Novikov coordinates.

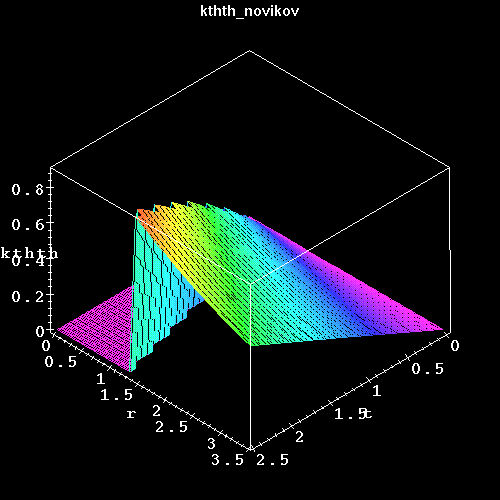
Finally, we show the error between the two solutions. Notice the rapidly growing error at the inner horizon which is intermittently truncated as grid points fall into the horizon. Also notice the warping of the outer edge which propagates inward over time.